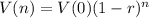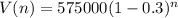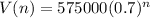Question

A company buys a machine for $575,000 that depreciates at a rate of 30% per year. Find a formula for the value of the machine after n years. V(n)

Answer 1

`V(n) = 575000(0.7)^(n)`

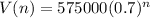
Explanation:

The value of the machine after n years is given by an exponential function in the following format:

`V(n) = V(0)(1-r)^(n)`

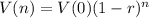
In which V(0) is the initial value and r is the yearly rate of depreciation, as a decimal.

A company buys a machine for $575,000 that depreciates at a rate of 30% per year.

This means, respectively, that:
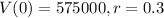`V(0) = 575000, r = 0.3`. So

`V(n) = V(0)(1-r)^(n)`

`V(n) = 575000(1-0.3)^(n)`

`V(n) = 575000(0.7)^(n)`