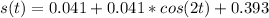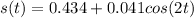Answer:
The expression of s(t) using double-angle identity is
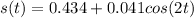
Explanation:
From the question we are told that
The sales of a computer manufacturer during 2015-2017 is approximated by the function
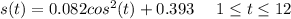
Now applying the double-angle to express s (t) in terms of the cosine function we have
![s(t) = 0.082 [(1 + cos(2t))/(2) ] + 0.3931](https://img.qammunity.org/2021/formulas/mathematics/college/eejs1k9mumk8tp9austf6dmv57o0fqneft.png) Note that
Note that
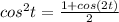
![s(t) = (0.082)/(2) [1 + cos(2t) ] + 0.393](https://img.qammunity.org/2021/formulas/mathematics/college/r0orbo6fcb1gasqxkfu85te3sr6w8wzemb.png)
![s(t) = 0.041 [1 + cos(2t) ] + 0.393](https://img.qammunity.org/2021/formulas/mathematics/college/oymhai8jepet9s12k0ulcbbr0mvyw9ybl7.png)