Question

Se desea plantar árboles a lo largo de un camino de 80m de longitud, a una distancia mínima entre ellos. Si dicha distancia de separación aumentará 6m, entonces el número de árboles necesarios disminuirá en 3. ¿Cuántos árboles serán plantados de la primera forma?

Answer 1

Answer: 8 arboles.

Explanation:

Ok, el camino tiene 80m de longitud.

Si la distancia entre árbol y árbol es x metros, entonces entran:

N = 80m/x arboles.

Ahora, si x aumenta en 6m, entonces el numero de arboles se reduciría en 3, entonces tenemos el sistema de ecuaciones:

N = 80/x

N - 3 = 80/(x + 6)

Para resolver esto, el primer paso es remplazar la primera ecuación en la segunda:

N - 3 = 80/x - 3 = 80/(x +6)

Ahora podemos resolver esto para x.

80*(x + 6) - 3*x*(x +6) = 80x

80*x + 480 - 3*x^2 - 18*x - 80x = 0

-3*x^2 -18*x + 480 = 0

necesitamos resolver esa ecuación cuadrática, y sabemos que las soluciones son:

`x = (18 +-√(18^2 + 4*3*480) )/(-2*3) = (18 +-78)/(-6)`

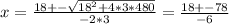
Entonces las dos soluciones son:

x = (18 +78)/-6 = -16

x = (18 - 78)/-6 = 10

La solución tiene que ser positiva, así que elegimos la segunda.

Esto quiere decir que la primera distancia es 10 metros, entonces el numero de arboles es:

N = 80m/10m = 8