Question

An ice skater spinning with outstretched arms has an angular speed of 5.0 rad/s . She tucks in her arms, decreasing her moment of inertia by 11 % . By what factor does the skater's kinetic energy change? (Neglect any frictional effects.)

Answer 1

K_{f} / K₀ =1.12

Step-by-step explanation:

This problem must work using the conservation of angular momentum (L), so that the moment is conserved in the system all the forces must be internal and therefore the torque is internal and the moment is conserved.

Initial moment. With arms outstretched

L₀ = I₀ w₀

the wo value is 5.0 rad / s

final moment. After he shrugs his arms

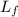`L_(f)` = I_{f} w_{f}

indicate that the moment of inertia decreases by 11%

I_{f} = I₀ - 0.11 I₀ = 0.89 I₀

L_{f} = L₀

I_{f} w_{f} = I₀ w₀

w_{f} = I₀ /I_{f} w₀

let's calculate

w_{f} = I₀ / 0.89 I₀ 5.0

w_{f} = 5.62 rad / s

Having these values ​​we can calculate the change in kinetic energy

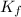`K_(f)` / K₀ = ½ I_{f} w_{f}² (½ I₀ w₀²)

K_{f} / K₀ = 0.89 I₀ / I₀ (5.62 / 5)²

K_{f} / K₀ =1.12