Answer:
-128
Step-by-step explanation:
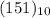
We have to convert this decimal number into the binary number
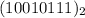
Performing the 2's complement number so we have to subtract 1 from this
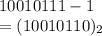
Now to getting the original number we have to complement the previous number it means convert 1 ->0 and 0 -> 1

The previous number is converted binary to decimal we get ,
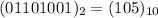
-105(According to the rule of 2's complement )
Similarly same process will apply on the
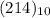
We have to convert this decimal number into the binary number
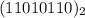
Performing the 2's complement number so we have to subtract 1 from this
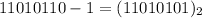
Now to getting the original number we have to complement the previous number it means convert 1 ->0 and 0 -> 1

The previous number is converted binary to decimal we get ,

-42(According to the rule of 2's complement )
Therefore the result is
151 + 214
=(-105 + (-42)
=-147
Hence the -147 is smaller then -128 that is smaller 8 bit signed integer is Therefore result is : -128