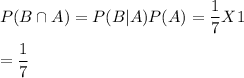Question

Assume that the year has 366 days and all birthdays are equally likely. Find the probability that two people chosen at random were born on the same day of the week.

Answer 1

`(1)/(7)`

Explanation:

There are 7 days in a week.

For the first person, we select one day out of the 7 days. The first person has 7 options out of the 7 days.

Let Event A be the event that the first person was born on a day of the week.

Therefore:

`P(A)=(7)/(7)=1`

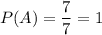
The second person has to be born on the same day as the first person. Therefore, the second person has 1 out of 7 days to choose from.

Let Event B be the event that the second person was born.

Therefore, the probability that the second person was born on the same day as the first person:

`P(B|A)=(1)/(7)`

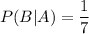
By the definition of Conditional Probability

`P(B|A)=(P(B \cap A))/(P(A)) \\$Therefore:\\P(B \cap A)=P(B|A)P(A)`

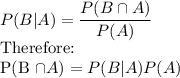
The probability that both were born on the same day is:

`P(B \cap A)=P(B|A)P(A) = (1)/(7) X 1 \\\\= (1)/(7)`