Question

In a​ poll, 37​% of the people polled answered yes to the question​ "Are you in favor of the death penalty for a person convicted of​ murder?" The margin of error in the poll was 5​%, and the estimate was made with 94​% confidence. At least how many people were​ surveyed?

Answer 1

329 people were​ surveyed

Explanation:

Percent of people polling yes to the question​ "Are you in favor of the death penalty for a person convicted of​ murder?"= 37 %

Margin error in the poll=5%

Confidence Interval=94%

The alpha value =1-0.94= 0.06

The Z ( critical value) for Confidence Interval of 94% =1.88

The sample size is given by

`n=pq((z)/(e))^2`

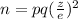
where, p=0.37, q=0.63, e= 5/100= 0.05, z=1.88

therefore,

`n=0.37*0.63((1.88)/(0.05))^2`

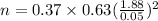
=329.54745

=329 people were​ surveyed

Answer 2

The number of people ​surveyed was 330.

Explanation:

The (1 - α)% confidence interval for the population proportion is:

`CI=\hat p\pm z_(\alpha/2)\cdot \sqrt{(\hat p(1-\hat p))/(n)}`

The margin of error for this interval is:

`MOE= z_(\alpha/2)\cdot \sqrt{(\hat p(1-\hat p))/(n)}`

The information provided is:

`\hat p=0.37\\MOE=0.05\\\text{Confidence level}=0.94\\\Rightarrow \alpha=0.06`

The critical value of z for 94​% confidence level is, z = 1.88.

*Use a z-table.

Compute the value of n as follows:

`MOE= z_(\alpha/2)\cdot \sqrt{(\hat p(1-\hat p))/(n)}`

`n=[(z_(\alpha/2)* √(\hat p(1-\hat p)))/(MOE)]^(2)`

`=[(1.88* √(0.37(1-0.37)))/(0.05)]^(2)\\\\=(18.153442)^(2)\\\\=329.5475\\\\\approx 330`

Thus, the number of people ​surveyed was 330.