Question

During the time a compact disc (CD) accelerates from rest to a constant rotational speed of 477 rev/min, it rotates through an angular displacement of 1.5758 rev. What is the angular acceleration of the CD

Answer 1

126.01 rad/s^2

Step-by-step explanation:

since it starts from rest, initial angular speed ω' = 0 rad/s

angular speed N = 477 rev/min

angular speed in rad/s ω =
`(2\pi N)/(60)` =
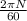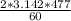`(2*3.142* 477)/(60)` = 49.95 rad/s

angular displacement ∅ = 1.5758 rev

angular displacement in rad/s =
`2\pi N` = 2 x 3.142 x 1.5758 = 9.9 rad

angular acceleration
`\alpha` = ?

using the equation of angular motion

ω^2 = ω'^2 + 2
`\alpha`∅

imputing values, we have

`49.95^(2) = 0^(2) + (2 *\alpha*9.9 )`

2495 = 19.8
`\alpha`

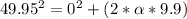
`\alpha` = 2495/19.8 = 126.01 rad/s^2