Answer:
The power produced by the turbine is 23309.1856 kW
Step-by-step explanation:
h₁ = 3755.39
s₁ = 7.0955
s₂ = sf + x₂sfg =
Interpolating fot the pressure at 3.25 bar gives;
570.935 +(3.25 - 3.2)/(3.3 - 3.2)*(575.500 - 570.935) = 573.2175
2156.92 +(3.25 - 3.2)/(3.3 - 3.2)*(2153.77- 2156.92) = 2155.345
h₂ = 573.2175 + 0.94*2155.345 = 2599.2418 kJ/kg
Power output of the turbine formula =
![Q - \dot{W } = \dot{m}\left [ \left (h_(2)-h_(1) \right )+(v_(2)^(2)- v_(1)^(2))/(2) + g(z_(2)-z_(1))\right ]](https://img.qammunity.org/2021/formulas/engineering/college/nho946yhzy2mp9rr61erc8fmzid5i2nji2.png)
Which gives;
![560 - \dot{W } = 8\left [ \left (2599.2418-3755.39 \right )+(15^(2)- 60^(2))/(2) \right ]](https://img.qammunity.org/2021/formulas/engineering/college/jp3tj725opqtwbvmd0eb04dkbkp0hnu4ag.png)
= -8*((2599.2418 - 3755.39)+(15^2 - 60^2)/2 ) = -22749.1856
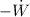 = -22749.1856 - 560 = -23309.1856 kJ
= -22749.1856 - 560 = -23309.1856 kJ
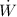 = 23309.1856 kJ
= 23309.1856 kJ
Power produced by the turbine = Work done per second = 23309.1856 kW.