Question

A 10 gauge copper wire carries a current of 23 A. Assuming one free electron per copper atom, calculate the magnitude of the drift velocity of the electrons.

Answer 1

Question:

A 10 gauge copper wire carries a current of 15 A. Assuming one free electron per copper atom, calculate the drift velocity of the electrons. (The cross-sectional area of a 10-gauge wire is 5.261 mm².)

Answer:

3.22 x 10⁻⁴ m/s

Step-by-step explanation:

The drift velocity (v) of the electrons in a wire (copper wire in this case) carrying current (I) is given by;

v =
`(I)/(nqA)`

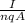
Where;

n = number of free electrons per cubic meter

q = electron charge

A = cross-sectional area of the wire

First let's calculate the number of free electrons per cubic meter (n)

Known constants:

density of copper, ρ = 8.95 x 10³kg/m³

molar mass of copper, M = 63.5 x 10⁻³kg/mol

Avogadro's number, Nₐ = 6.02 x 10²³ particles/mol

But;

The number of copper atoms, N, per cubic meter is given by;

N = (Nₐ x ρ / M) -------------(ii)

Substitute the values of Nₐ, ρ and M into equation (ii) as follows;

N = (6.02 x 10²³ x 8.95 x 10³) / 63.5 x 10⁻³

N = 8.49 x 10²⁸ atom/m³

Since there is one free electron per copper atom, the number of free electrons per cubic meter is simply;

n = 8.49 x 10²⁸ electrons/m³

Now let's calculate the drift electron

Known values from question:

A = 5.261 mm² = 5.261 x 10⁻⁶m²

I = 23A

q = 1.6 x 10⁻¹⁹C

Substitute these values into equation (i) as follows;

v =
`(I)/(nqA)`

v =
`(23)/(8.49*10^(28) * 1.6 *10^(-19) * 5.261*10^(-6))`

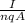
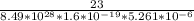
v = 3.22 x 10⁻⁴ m/s

Therefore, the drift electron is 3.22 x 10⁻⁴ m/s