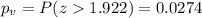Question

A human resources representative claims that the proportion of employees earning more than $50,000 is less than 40%. To test this claim, a random sample of 700 employees is taken and 305 employees are determined to earn more than $50,000.The following is the setup for this hypothesis test:{H0:p=0.40Ha:p<0.40Find the test statistic for this hypothesis test for a proportion. Round your answer to 2 decimal places.

Answer 1

The statistic for this case would be:

`z=\frac{\hat p -p_o}{\sqrt{(\hat p(1-\hat p))/(n)}}`

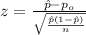
And replacing we got:

`z= \frac{0.436-0.4}{\sqrt{(0.436*(1-0.436))/(700)}}= 1.92`

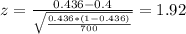
Explanation:

For this case we have the following info:

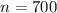`n =700` represent the sample size

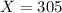`X= 305` represent the number of employees that earn more than 50000

`\hat p=(305)/(700)= 0.436`

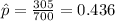
We want to test the following hypothesis:

Nul hyp.
`p \leq 0.4`

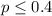
Alternative hyp :
`p>0.4`

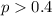
The statistic for this case would be:

`z=\frac{\hat p -p_o}{\sqrt{(\hat p(1-\hat p))/(n)}}`

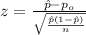
And replacing we got:

`z= \frac{0.436-0.4}{\sqrt{(0.436*(1-0.436))/(700)}}= 1.92`

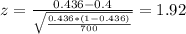
And the p value would be given by:

`p_v = P(z>1.922)= 0.0274`