Question

Joe takes out a 30-year fixed rate amortized loan for 220,000, and makes equal size payments at the end of each month. The rate is quoted as being an annual nominal interest rate of 5.25% compounded monthly and Joe also has to pay closing fees equal to 5% of the value of the loan. Based on this information, find the actual interest rate realized by Joe (i.E. Taking into account the loan given to Joe and the 5% that he pays for the closing fees). Give the value as an annual nominal rate compounded monthly, and round your percent answer to two decimal places.

Answer 1

Annual Interest Rate, r = 5.69%

Explanation:

Amount of loan taken = 220,000

Closing fee is 5% of the loan value

Closing fee = 5% of 222,000 = 0.05 * 220000 = 11000

Therefore, Principal, P = Loan amount + closing fee

P = 220000 + 11000

P = 231, 000

Annual rate, r= 5.25% = 0.0525

Monthly rate, i = 0.0525/12 = 0.004375

Time, n = 30 years = 30*12 = 360 months

The monthly payment will be calculated by:

`PMT = (P*i)/(1 - (1 + i)^(-n)) \\\\PMT = (231000 * 0.004375)/(1 - (1 + 0.004375)^(-360)) \\\\PMT = 1275.59`

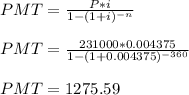
Assuming payments are made based on 220,000, let us calculate the monthly interest rate.

`PMT = (P*i)/(1 - (1 + i)^(-n)) \\\\1275.59 = (220000 * i)/(1 - (1 + i)^(-360)) \\\\i = 0.00474229`

Annual rate, r = 12 * 0.0047429

r = 0.0569 = 5.69%