Question

excel A car insurance company has determined that 8% of all drivers were involved in a car accident last year. If 15 drivers are randomly selected, what is the probability of getting 3 or more who were involved in a car accident last year

Answer 1

`P(X \geq 3)= 1- P(X<3)= 1-P(X \leq 2)= 1- [P(X=0) +P(X=1) +P(X=2)]`

And we can find the individual probabilites using the probability mass function and we got:

`P(X=0) = (15C0) (0.08)^(0) (1-0.08)^(15-0)=0.286`

`P(X=1) = (15C1) (0.08)^(1) (1-0.08)^(15-1)=0.373`

`P(X=2) = (15C2) (0.08)^(2) (1-0.08)^(15-2)=0.227`

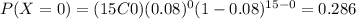
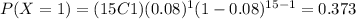
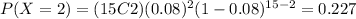
And replacing we got:

`P(X\geq 3) = 1-[0.286+0.373+0.227 ]= 0.114`

Explanation:

For this case we can assume that the variable of interest is "drivers were involved in a car accident last year" and for this case we can model this variable with this distribution:

`X \sim Bin (n =15, p =0.08)`

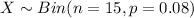
And for this case we want to find this probability;

`P(X \geq 3)`

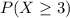
and we can use the complement rule and we got:

`P(X \geq 3)= 1- P(X<3)= 1-P(X \leq 2)= 1- [P(X=0) +P(X=1) +P(X=2)]`

And we can find the individual probabilites using the probability mass function and we got:

`P(X=0) = (15C0) (0.08)^(0) (1-0.08)^(15-0)=0.286`

`P(X=1) = (15C1) (0.08)^(1) (1-0.08)^(15-1)=0.373`

`P(X=2) = (15C2) (0.08)^(2) (1-0.08)^(15-2)=0.227`

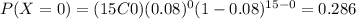
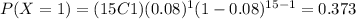
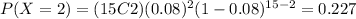
And replacing we got:

`P(X\geq 3) = 1-[0.286+0.373+0.227 ]= 0.114`