Answer:
Option B.
Explanation:
If a line passing through two points, then the slope of line is
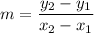
It is given that f(x) passing through the points (0,-2) and (1,1). So, slope of f(x) is
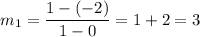
It is given that g(x) passing through the points (-4,0) and (0,2). So, slope of g(x) is
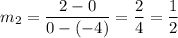
Since,
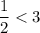 , therefore
, therefore
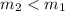 .
.
The slope of g(x) is less than the slope of f(x).
Therefore, the correct option is B.