Question

Find the missing length to the nearest tenth.
Right Triangle
6 m
C
16 m

Answer 1

17.1 meters

Explanation:

Since this is a right triangle, we can use the Pythagorean Theorem.

`a^2+b^2=c^2`

where a and b are the legs and c is the hypotenuse.

6 and 16 are the legs, because they form the right angle. c is the hypotenuse because it is opposite the right angle.

`6^2+16^2=c^2`

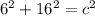
Evaluate the exponents.

6^2= 6*6= 36

16^2= 16*16= 256

`36+256=c^2`

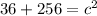
Add 36 and 256.

`292=c^2`

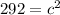
Since c is being squared, take the square root of both sides of the equation. The exponent and square root will cancel and leave c by itself

`√(292) =√(c^2)`

`√(292)=c`

`17.0880075=c`

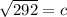
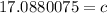
Round to the nearest tenth. The 8 in the hundredeth place tells us to roung the 0 in the tenth place up to a 1.

`17.1=c`

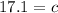
c= 17.1 m

The missing length, or the hyptenuse is 17.1 meters.