Question

Education: 3/2 t- 16 = 4/3 t - 6 How do I get that both variables stay at left side .

Answer 1

`t=60`

Explanation:

To get both variables on one side, do the opposite of their current form and move them over (I'm not sure how else to explain this, so I'm just going to show you).

`(3)/(2) t-16=(4)/(3) t-6`

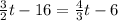
You see that the
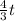`(4)/(3) t` is positive, so you subtract it. The same goes for the -16 (do the opposite). You would add the -16 to the other side.

You need to do the opposite of them because only one number exists. If you move it, you need to cancel it out so that there is always only one of that number. (so when you add the -16 to the other side, the one on the left cancels out, but the same value (16) is still present on the right side and is added).

`(3)/(2) t-(4)/(3) t=-6+16`

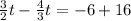
Now you have this after moving like terms to their coinciding sides (you could do this any way, btw. It doesn't matter what order you add everything, so long as you get t on one side and by itself).

`(9)/(6) t-(8)/(6)t =-6+16\\(1)/(6) t=10\\((6)/(1) )((1)/(6) t)=((6)/(1) )(10)\\t=60`

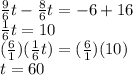
** Everything you do on one side, you need to do on the other side. This is a very important rule (and it goes hand in hand with the idea that there can only be one of each value, unless the exact same value appeared on both sides in the given equation).

Answer 2

60

Explanation:

3/2t-16=4/3t-6

+16 +16

3/2t=4/3t+10

-4/3t

(t/6)6/1= 10(6/1)

t=60