Question

1. Write the standard form of the line that passes through the given points. (7, -3) and (4, -8)

2. Write the equation of the line, in standard form, that has a y-intercept of 2 and is parallel to 2 x + y = -5.
3. Write the equation of the line, in standard form, that has an x-intercept of 2 and is parallel to 2x + y = -5

Answer 1

1.
`-5x+3y+44=0`

2.
`2x+y-2=0`

3.
`2x+y-4=0`

Explanation:

Standard form of a line is
`Ax+By+C=0`.

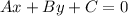If a line passing through two points then the equation of line is

`y-y_1=m(x-x_1)`

where, m is slope, i.e.,
`m=(y_2-y_1)/(x_2-x_1)`.

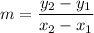1.

The line passes through the points (7,-3) and (4,-8). So, the equation of line is

`y-(-3)=(-8-(-3))/(4-7)(x-7)`

`y+3=(-5)/(-3)(x-7)`

`y+3=(5)/(3)(x-7)`

`3(y+3)=5(x-7)`

`3y+9=5x-35`

`-5x+3y+9+35=0`

`-5x+3y+44=0`

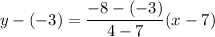
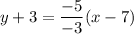
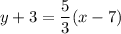
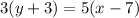
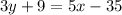
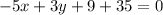
Therefore, the required equation is
`-5x+3y+44=0`.

2.

We need to find the equation of the line, in standard form, that has a y-intercept of 2 and is parallel to
`2 x + y =-5`.

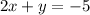Slope of the line :
`m=\frac{-\text{Coefficient of x}}{\text{Coefficient of y}}=(-2)/(1)=-2`

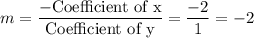
Slope of parallel lines are equal. So, the slope of required line is -2 and it passes through the point (0,2).

Equation of line is

`y-2=-2(x-0)`

`y-2=-2x`

`2x+y-2=0`

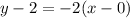
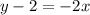
Therefore, the required equation is
`2x+y-2=0`.

3.

We need to find the equation of the line, in standard form, that has an x-intercept of 2 and is parallel to
`2x + y =-5`.

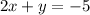From part 2, the slope of this line is -2. So, slope of required line is -2 and it passes through the point (2,0).

Equation of line is

`y-0=-2(x-2)`

`y=-2x+4`

`2x+y-4=0`

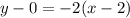
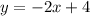
Therefore, the required equation is
`2x+y-4=0`.