Answer:
See explanation
Step-by-step explanation:
Solution:-
- Here we will assume that the grating has the line density ( N ) defined by the number of lines per mm.
- The angle that each fringe forms on the screen is defined by ( θ ).
- The order of bright/dark spot is defined by an integer ( n )
- The wavelength of the incident light is ( λ )
- Here we will use the relation given for diffraction grating by the Young's Experiment as follows:
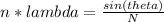
- The above given formulation is for constructive interference.
- We will inspect the effect of increasing the distance between the screen and the grating. Consider the length ( L ) from the center of the grating to the center of the screen. The distance ( yn ) will denote the distance between each fringe in vertical direction on the screen.
- For small angles ( θ ) we can make an approximation of sin ( θ ) ≈ tan ( θ ). Where,
sin ( θ ) ≈ tan ( θ ) = [ yn / L ]
- Substitute the above approximation in the given relation of diffraction gratings as follows:
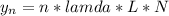
- To double the distance between the screen and grating we will use the above relation with ( 2L ):
yn ∝ L
Result: The distance between each order of bright and dark fringe is doubled. The interference pattern would have twice the spread! This also means that less number of bright spots would be seen on the screen as the coverage area would require a larger screen to accommodate the entire interference pattern. The spread also reduces the intensity/contrast between the bright and dark fringes because the distance travelled by each ray of light has increased. The intensity is inversely proportional to the square of distance travelled.
- Similarly, the line density of the grating ( N ) was doubled. Then,
yn ∝ N
Result: The distance between each order of bright and dark fringe is doubled. The interference pattern would have twice the spread!This also means that less number of bright spots would be seen on the screen as the coverage area would require a larger screen to accommodate the entire interference pattern.