Question

A 30,000-kg freight car is coasting at 2.00 m/s with negligible friction under a hopper that dumps 110,000 kg of scrap metal into it. How much kinetic energy is lost

Answer 1

47057J

Step-by-step explanation:

To get the kinetic energy lost, first let's calculate the final velocity (v) of the loaded freight car.

Since friction is negligible, we can use the law of conservation of momentum to get the final velocity as follows;

m₁ u₁ + m₂ u₂ = (m₁ + m₂) v -----------------(i)

Where;

m₁ = mass of the freight car initially = 30000kg

m₂ = mass of the scrap metal = 110000kg

u₁ = initial velocity of the car = 2.00m/s

u₂ = initial velocity of the scrap metal = 0m/s {since the metal was at rest}

Substitute these values into equation (i) as follows;

(30000 x 2.00) + (110000 x 0) = (30000 + 110000)v

60000 + 0 = 140000v

60000 = 140000v

v =
`(60000)/(140000)`

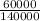
v = 0.43m/s

Now,

The initial kinetic energy (KE₀) of the system of freight car and scrap metal is given by;

KE₀ =
`(1)/(2)`m₁ u₁² +
`(1)/(2)`m₂ u₂² ----------------(ii)

Substitute the right values into equation (ii)

KE₀ =
`(1)/(2)` (30000 x 2.00²) +
`(1)/(2)` (110000 x 0²)

KE₀ = 60000J

Also,

The final kinetic energy (KE₁) of the system of freight car and scrap metal is given by;

KE₁ =
`(1)/(2)`(m₁ + m₂) v² ----------------(iii)

Substitute the right values into equation (iii)

KE₁ =
`(1)/(2)`(30000 + 110000) x 0.43²

KE₁ = 12943J

The loss in kinetic energy (K) is therefore given by the difference between the initial and final values of the kinetic energy.

K = KE₁ - KE₀

K = 12943 - 60000

K = -47057J [negative sign shows that energy was lost]

Therefore, the loss in kinetic energy is 47057J