Question

The owner of a car wash wants to see if the arrival rate of cars follows a Poisson distribution. In order to test the assumption of a Poisson distribution, a random sample of 150 ten-minute intervals was taken. You are given the following observed frequencies: Number of Cars Arriving in a 10-Minute Interval Frequency 0 3 1 10 2 15 3 23 4 30 5 24 6 20 7 13 8 8 9 or more 4 150 Calculate mean and use Poisson probabilities. The expected frequency of exactly 3 cars arriving in a 10-minute interval is a. .1533. b. 26.145. c. .1743. d. 23.

Answer 1

Answer: c. 0.1743

Explanation: Poisson Probability or Poisson Distribution is a discrete distribution that models the number of events ocurring in a given period of time.

The mean, or expected value, of the observed frequencies is:

E(X) = ∑xP(x)

E(X) = 0*3/150 + 1*(10/150) + 2*(15/150) + 3*(23/150) + 4*(30/150) + 5*(24/150) + 6*(20/150) + 7*(13/150) + 8*(8/150) + 9*(4/150)

E(X) = 4.399

The Poisson distribution is calculated by:

P(X = k) =
`(mean^(k).e^(-mean))/(k!)`

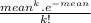
The question asks for the expected frequency of exactly 3 cars:

P(X = 3) =
`(4.399^(3).e^(-4.399))/(3!)`

P(X = 3) =
`(4.399^(3).e^(-4.399))/(3.2.1)`

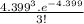
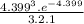
P(X = 3) = 0.1743

The expected frequency of exactly 3 cars is 0.1743