Question

According to Advertising Age, the average base salary for women working as copywriters in advertising firms is higher than the average base salary for men. The average base salary for women is $67,000 and the average base salary for men is $65,500 (Working Woman, July/August 2000). Assume salaries are normally distributed and that the standard deviation is $7000 for both men and women.

Required:
a. What is the probability of a woman receiving a salary in excess of $75,000 (to 4 decimals)?
b. What is the probability of a man receiving a salary in excess of $75,000 (to 4 decimals)?
c. What is the probability of a woman receiving a salary below $50,000 (to 4 decimals)?
d. How much would a woman have to make to have a higher salary than 99% of her male counterparts (0 decimals)?

Answer 1

(a) The probability of a woman receiving a salary in excess of $75,000 is 0.1271.

(b) The probability of a man receiving a salary in excess of $75,000 is 0.0870.

(c) The probability of a woman receiving a salary below $50,000 is 0.9925.

(d) A woman would have to make a higher salary of $81,810 than 99% of her male counterparts.

Explanation:

Let the random variable X represent the salary for women and Y represent the salary for men.

It is provided that:

`X\sim N(67000, 7000^(2))\\\\Y\sim N(65500, 7000^(2))`

(a)

Compute the probability of a woman receiving a salary in excess of $75,000 as follows:

`P(X>75000)=P((X-\mu_(x))/(\sigma_(x))>(75000-67000)/(7000))`

`=P(Z>1.14)\\\\=1-P(Z<1.14)\\\\=1-0.87286\\\\=0.12714\\\\\approx 0.1271`

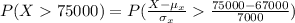
Thus, the probability of a woman receiving a salary in excess of $75,000 is 0.1271.

(b)

Compute the probability of a man receiving a salary in excess of $75,000 as follows:

`P(Y>75000)=P((Y-\mu_(y))/(\sigma_(y))>(75000-65500)/(7000))`

`=P(Z>1.36)\\\\=1-P(Z<1.36)\\\\=1-0.91309\\\\=0.08691\\\\\approx 0.0870`

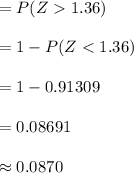
Thus, the probability of a man receiving a salary in excess of $75,000 is 0.0870.

(c)

Compute the probability of a woman receiving a salary below $50,000 as follows:

`P(X<50000)=P((X-\mu_(x))/(\sigma_(x))<(50000-67000)/(7000))`

`=P(Z>-2.43)\\\\=P(Z<2.43)\\\\=0.99245\\\\\approx 0.9925`

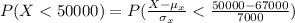
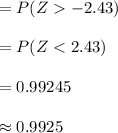
Thus, the probability of a woman receiving a salary below $50,000 is 0.9925.

(d)

Let a represent the salary a woman have to make to have a higher salary than 99% of her male counterparts.

Then,

`P(Y\leq a)=0.99`

`\Rightarrow P(Z<z)=0.99`

The z-score for this probability is:

z-score = 2.33

Compute the value of a as follows:

`(a-\mu_(y))/(\sigma_(y))=2.33\\\\`

`a=\mu_(y)+(2.33* \sigma_(y))\\\\`

`=65500+(2.33*7000)\\\\=65500+16310\\\\=81810`

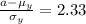
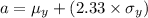
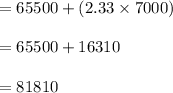
Thus, a woman would have to make a higher salary of $81,810 than 99% of her male counterparts.