Question

how many different four letter permutations can be formed using four letters out of the first 12 in the alphabet?

Answer 1

Answer: it’s 11,880

not 11800

Answer 2

11,800 different four letter permutations can be formed using four letters out of the first 12 in the alphabet

Explanation:

Permutations formula:

The number of possible permutations of x elements from a set of n elements is given by the following formula:

`P_((n,x)) = (n!)/((n-x)!)`

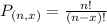
In this question:

Permutations of four letters from a set of 12 letters. So

`P_((12,4)) = (12!)/((12-4)!) = 11800`

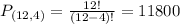
11,800 different four letter permutations can be formed using four letters out of the first 12 in the alphabet