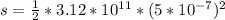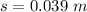Complete Question
A proton of mass mp= 1.67×10−27 kg and a charge of qp= 1.60×10−19 C is moving through vacuum at a constant velocity of 10,000 m/s directly to the east when it enters a region of uniform electric field that points to the south with a magnitude of E = 3.62e+3 N/C . The region of uniform electric field is 5 mm wide in the east-west direction. How far (in meters) will the proton have been deflected towards the south by the time it exits the region of uniform electric field. You may neglect the effects of friction and gravity, and assume that the electric field is zero outside the specified region. Answer is to be in units of meters
Answer:
Step-by-step explanation:
From the question we are told that
The mass of the proton is
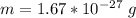
The charge of on the proton is

The speed of the proton is
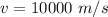
The magnitude of the electric field is

The width covered by the electric field

Generally the acceleration of the proton due to the electric toward the south (at the point where the force on the proton is equal to the electric force due to the electric field) is mathematically represented as

Substituting values
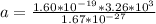
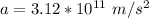
Generally the time it will take the proton to cross the electric field is mathematically represented as
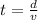
Substituting values
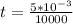
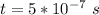
Generally the the distance covered by the proton toward the south is
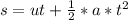
Here u = 0 m/s this because before the proton entered the electric field region the it velocity towards the south is zero
So
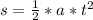
Substituting values