Question

Find the directional derivative of f at the given point in the direction indicated by the angle θ. f(x, y) = y cos(xy), (0, 1), θ = π/6

Answer 1

1/2

Explanation:

The directional derivative of f at the given point in the direction indicated by the angle θ is expressed as
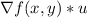`\\abla f(x, y)*u` where u is the unit vector in the direction θ.

Lets first calculate
`\\abla f(x, y)\ at\ (0, 1)`

`\\abla = (\delta)/(\delta x) i + (\delta)/(\delta y) j \\\\abla f(x, y) = (\delta (y cos(xy)))/(\delta x) i + (\delta(y cos(xy)))/(\delta y) j\\\\abla f(x, y)= -y^(2) sinxy\ i + (cosxy -xysinxy) j\\`

`\\abla f(x, y)\ at\ (0, 1)\\= -1^(2)sin0 \ i +(cos 0 - 0sin0) \j\\= 0i+j\\\\`

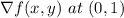
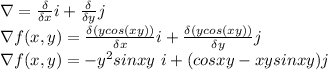
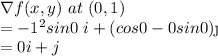
The unit vector u in the direction of θ is expressed as
`cos\theta \ i + sin\theta \ j`

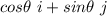
unit vector u at θ = π/6 is cos π/6i + sin π/6 j

u= √3/2 i +1/2 j

Taking the dot product i.e
`\\abla f(x, y)*u`

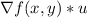
= (0i+j)*(√3/2 i +1/2 j)

= 1/2

The directional derivative of f is 1/2