A roof has a cross section that is a right triangle. The diagram shows the approximate dimensions of this cross section. Find the height h of the roof. Round your answer to the …

Question

asked Jul 23, 2021 204k views

2 Answers

Crrmacarse · Answer 1 · 2021-07-27T08:03:09+0000

Answer:

The height of the roof is 25 ft.

Explanation:

Consider the right angled triangle BCD.

Determine the measure of side BD using the Pythagoras theorem

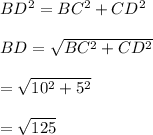
$BD^(2)=BC^(2)+CD^(2)\\\\BD=\sqrt{BC^(2)+CD^(2)}\\\\=\sqrt{10^(2)+5^(2)}\\\\=√(125)$

Compute the measure of angle x as follows:

$tan\ x=(BC)/(CD)\\\\tan\ x=(10)/(5)\\\\tan\ x=2\\\\x=tan^(-1)2\\\\x=63.4$

Now consider the triangle ABD.

The hypotenuse AD is the height of the roof.

Determine the measure of side AD as follows:

$cos\ x=(BD)/(AD)\\\\cos\ 63.4=(√(125))/(AD)\\\\0.4478=(√(125))/(AD)\\\\AD=(√(125))/(0.4478)\\\\AD=24.967\\\\AD\approx 25$

Thus, the height of the roof is 25 ft.