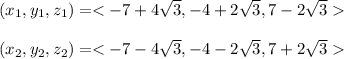Question

if the line〈3 + 2t,1 +t,2−t〉intersects the unit sphere inR3given byx2+y2+z2= 1,and if so, at what points.

Answer 1

`( x_1 , y_1 , z_1 ) = < -7 + 4√(3) , -4 + 2√(3) , 7 - 2√(3) >\\\\( x_2 , y_2 , z_2 ) = < -7 - 4√(3) , -4 - 2√(3) , 7 + 2√(3) >\\`

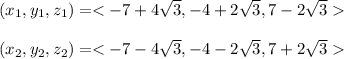
Explanation:

Solution:-

- We are given a parametric form for the vector equation of line defined by ( t ).

- The line vector equation is:

L: < 3 + 2t , t + 1 , 2 -t >

- The same 3-dimensional space is occupied by a unit sphere defined by the following equation:

`S: x^2 + y^2 + z^2 = 1`

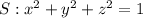
- We are to determine the points of intersection of the line ( L ) and the unit sphere ( S ).

- We will substitute the parametric equation of line ( L ) into the equation defining the unit sphere ( S ) and solve for the values of the parameter ( t ):

`( 3 + 2t )^2 + ( 1 + t )^2 + ( 2 - t)^2 = 1\\\\( 9 + 12t + 4t^2 ) + ( t^2 + 2t + 1 ) + ( 4 + t^2 -4t ) = 1\\\\t^2 + 10t + 13 = 0\\\\`

- Solve the quadratic equation for the parameter ( t ):

`t = -5 + 2√(3) , -5 - 2√(3)`

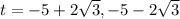
- Plug in each of the parameter value in the given vector equation of line and determine a pair of intersecting coordinates:

`( x_1 , y_1 , z_1 ) = < -7 + 4√(3) , -4 + 2√(3) , 7 - 2√(3) >\\\\( x_2 , y_2 , z_2 ) = < -7 - 4√(3) , -4 - 2√(3) , 7 + 2√(3) >\\`