Answer:
The work done by the force is 820.745 joules.
Step-by-step explanation:
Let suppose that changes in potential energy can be neglected. According to the Work-Energy Theorem, an external conservative force generates a change in the state of motion of the object, that is a change in kinetic energy. This phenomenon is describe by the following mathematical model:
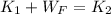
Where:
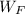 - Work done by the external force, measured in joules.
- Work done by the external force, measured in joules.
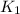 ,
,
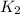 - Translational potential energy, measured in joules.
- Translational potential energy, measured in joules.
The work done by the external force is now cleared within:
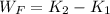
After using the definition of translational kinetic energy, the previous expression is now expanded as a function of mass and initial and final speeds of the object:
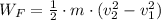
Where:
 - Mass of the object, measured in kilograms.
- Mass of the object, measured in kilograms.
 ,
,
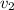 - Initial and final speeds of the object, measured in meters per second.
- Initial and final speeds of the object, measured in meters per second.
Now, each speed is the magnitude of respective velocity vector:
Initial velocity

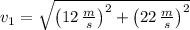
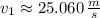
Final velocity
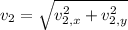

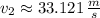
Finally, if
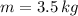 ,
,
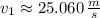 and
and
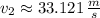 , then the work done by the force is:
, then the work done by the force is:
![W_(F) = (1)/(2)\cdot (3.5\,kg)\cdot \left[\left(33.121\,(m)/(s) \right)^(2)-\left(25.060\,(m)/(s) \right)^(2)\right]](https://img.qammunity.org/2021/formulas/physics/college/3jgukhajch11mf21fvvlet93nnocmem16h.png)

The work done by the force is 820.745 joules.