Question

power output of 87 W. At what distance will the decibel reading be 120 dB, which is noise level of a loud indoor rock concert

Answer 1

r = 2.63 m

Step-by-step explanation:

To find the distance at which the sound level is 120dB, you first calculate the intensity of the sound. You use the following formula:

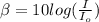`\beta=10log((I)/(I_o))` (1)

β: sound level = 120dB

I: intensity of the sound

Io: threshold of hearing = 10⁻12W/m^2

You solve the equation (1) for I and replace the values of all parameters:

`\beta=log((I)/(I_o))^(10)\\\\10^\beta=10^{log((I)/(I_o))^(10)}=((I)/(I_o))^(10)\\\\I=10^(\beta/10)I_o`

`I=10^(120/10)(10^(-12)W/m^2)=1(W)/(m^2)`

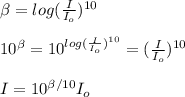
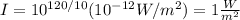
Next, you use the following formula for the power of the sound with intensity I, and you solve for r:

`I=(P)/(4\pi r^2)\\\\r=\sqrt{(P)/(4\pi I)}`

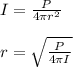
r: distance at which the sound level is 120dB

P: power of the sound = 87W

I: intensity of the sound = 1W/m^2

You replace the values of I and P for calculating r:

`r=\sqrt{(87W)/(4\pi (1W/m^2))}=2.63m`

The distance is at 2.63m from the source of the soundr = 2.63m