Question

An ultracentrifuge accelerates from rest to 100,000 rpm in 3.00 min. What is the tangential acceleration of a point 8.50 cm from the axis of rotation

Answer 1

4.95m/s²

Step-by-step explanation:

In rotational motion, the tangential acceleration (
`a_(t)`) is the product of the angular acceleration (∝) and the distance (r) from the axis of rotation and this is given by;

`a_(t)` = ∝r ------------------(i)

But the angular acceleration (∝) is the ratio of the angular velocity(ω) to time (t). i.e

∝ = ω / t

Substitute this into equation (i) as follows;

`a_(t)` = (ω/t)r ----------------(ii)

Now;

From the question;

ω = 100000rpm

Convert this to rad/s as follows;

ω =
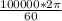`(100000 * 2\pi )/(60)` = 10473.3rad/s

t = 3.00min

Convert this to seconds as follows;

t = 3.00 x 60s = 180.0s

r = 8.50cm

Convert this to metres as follows

r =
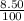`(8.50)/(100)` = 0.085m

Substitute these values into equation (ii) as follows;

`a_(t)` = (10473.3/180) (0.085)

`a_(t)` = 4.95m/s²

Therefore, the tangential acceleration is 4.95m/s²