Question

A d'Arsonal meter with an internal resistance of 1 kohm requires 10 mA to produce full-scale deflection. Calculate thew value of a series

Answer 1

Question:

A d’Arsonval meter with an internal resistance of 1 kΩ requires 10 mA to produce full-scale deflection. Calculate the value of a series resistance needed to measure 50 V of full scale.

Answer:

4kΩ

Step-by-step explanation:

Given;

internal resistance, r = 1kΩ

current, I = 10mA = 0.01A

Voltage of full scale, V = 50V

Since there is full scale voltage of 50V, then the combined or total resistance (R) of the circuit is given as follows;

From Ohm's law

V = IR

R =
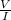`(V)/(I)` [substitute the values of V and I]

R =
`(50)/(0.01)`

R = 5000Ω = 5kΩ

The combined resistance (R) is actually the total resistance of the series arrangement of the series resistance(
`R_(S)`) and the internal resistance (r) in the circuit. i.e

R =
`R_(S)` + r

`R_(S)` = R - r [Substitute the values of R and r]

`R_(S)` = 5kΩ - 1kΩ

`R_(S)` = 4kΩ

Therefore the series resistance is 4kΩ