Question

Wanda exerts a constant tension force of 12 N on an essentially massless string to keep a tennis ball (m = 60 g) attached to the end of the string traveling in uniform circular motion above her head at a constant speed of 9.0 m/s. What is the length of the string between her hand and the tennis ball? You may ignore gravity in this problem (assume the motion of the tennis ball and string happen in a purely horizontal plane). A. 41 m B. 0.24 m C. 3.2 cm D. 0.41 m

Answer 1

r = 0.405m = 40.5cm

Step-by-step explanation:

In order to calculate the length of the string between Wanda and the ball, you take into account that the tension force is equal to the centripetal force over the ball. So, you can use the following formula:

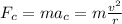`F_c=ma_c=m(v^2)/(r)` (1)

Fc: centripetal acceleration (tension force on the string) = 12N

m: mass of the ball = 60g = 0.06kg

r: length of the string = ?

v: linear speed of the ball = 9.0m/s

You solve for r in the equation (1) and replace the values of the other parameters:

`r=(mv^2)/(F_c)=((0.06kg)(9.0m/s)^2)/(12N)=0.405m`

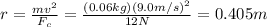
The length of the string between Wanda and the ball is 0.405m = 40.5cm