Question

The output S/N at thereceiver must be greater than 40 dB. The audio signal has zero mean, maximum amplitude of 1, power of ½ Wand bandwidth of 15 kHz. The power spectral density of white noise N0/2 = 10-10W/Hz and the power loss in the channel is 50 dB. Determine the transmit power required and the bandwidth needed.

Answer 1

Given that,

The output signal at the receiver must be greater than 40 dB.

Maximum amplitude = 1

Bandwidth = 15 kHz

The power spectral density of white noise is

`(N)/(2)=10^(-10)\ W/Hz`

Power loss in channel= 50 dB

Suppose, Using DSB modulation

We need to calculate the power required

Using formula of power

`P_(L)_(dB)=10\log(P_(L))`

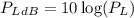
Put the value into the formula

`50=10\log(P_(L))`

`P_(L)=10^(5)\ W`

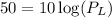
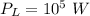
For DSB modulation,

Figure of merit = 1

We need to calculate the input signal

Using formula of FOM

`FOM=((S_(o))/(N_(o)))/((S_(i))/(N_(i)))`

`1=((S_(o))/(N_(o)))/((S_(i))/(N_(i)))`

`(S_(i))/(N_(i)W)=(S_(o))/(N_(o))`

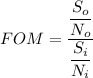
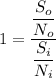
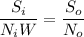
Put the value into the formula

`(S_(i))/(2*10^(-10)*15*10^(3))<40\ dB`

`(S_(i))/(30*10^(-7))<10^(4)`

`S_(i)<30*10^(-3)`

`S_(i)=30*10^(-3)`

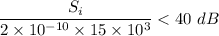
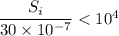
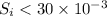
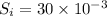
We need to calculate the transmit power

Using formula of power transmit

`S_(i)=(P_(t))/(P_(L))`

`P_(t)=S_(i)* P_(L)`

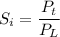
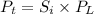
Put the value into the formula

`P_(t)=30*10^(-3)*10^(5)`

`P_(t)=3\ kW`

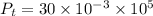
We need to calculate the needed bandwidth

Using formula of bandwidth for DSB modulation

`bandwidth=2W`

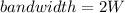
Put the value into the formula

`bandwidth =2*15`

`bandwidth = 30\ kHz`

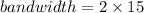
Hence, The transmit power is 3 kW.

The needed bandwidth is 30 kHz.