Answer:
36
Explanation:
As the triangle ABC is isosceles so A and B has the same measures
And, the sum of the angles is 180°.
Therefore 2 times the measure of angle
B plus 120° = 180°,
So, the equation:
2x + 120 = 180
So x = 30
Now we have to apply the law of sin on the triangle BMC as shown below:
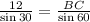
Now calculate for BC
BC = 20.7
We use the law of sin again i.e

So AB is 36