Answer:
T = 7.61*10^6 s
Step-by-step explanation:
In order to calculate the Mercury's period. in its orbit around the sun, you take into account on the Kepler's law. You use the following formula:
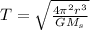 (1)
(1)
T: period of Mercury
r: distance between Mercury and Sun
Ms: mass of the sun = 1.98*10^30 kg
G: Cavendish's constant = 6.674*10^-11 m^3 kg^-1 s^-2
You replace the values of all parameters in the equation (1):
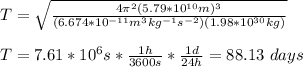
The period of Mercury is 7.61*10^6 s, which is approximately 88.13 Earth's days