Question

The plate OAB forms an equilateral triangle which rotates counterclockwise with increasing speed about point O. If the normal and tangential components of acceleration of the centroid C at a certain instant are 68 m/s2 and 22 m/s2, respectively, determine the values of and at this same instant. The angle θ is the angle between line AB and the fixed horizontal axis and the distance b = 160 mm.

Answer 1

the angular velocity θ' = 27.125 rad/s

the angular acceleration is θ'' = 238.044 rad/s²

Step-by-step explanation:

The plate OAB forms an equilateral triangle which rotates counterclockwise with increasing speed about point O.

If the normal and tangential components of acceleration of the centroid C at a certain instant are 68 m/s2 and 22 m/s2

From the distance (radius r) of the centroid C in the centre of the equilateral triangle to the point of rotation O; the position OC can be calculated as:

r = OC

`r = (2)/(3) \sqrt {160^2 - 80^2}`

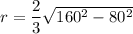
r = 0.667 × 138.564

r = 92.42 mm

r = 0.09242 m

However; the angular velocity can be determined by using the expression:

`a_n = \theta'^2 r`

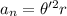
where;

`a_n` = normal acceleration = 68 m/s²

r = 0.09242 m

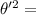`\theta'^2 =` angular velocity = ???

`68 = \theta'^2 * 0.09242`

`(68)/(0.09242) = \theta'^2`

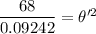
θ'² = 735.771478

θ' =
`√(735.771478)`

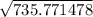
θ' = 27.125 rad/s

Thus; the angular velocity θ' = 27.125 rad/s

Similarly ; the angular acceleration can be determined as by the following relation:

`a_t = r \theta`

where;

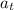`a_t` = tangential components of acceleration = 22 m/s²

r = 0.09242 m

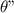`\theta` = angular acceleration

`22= 0.09242* \theta`

`(22)/(0.09242)= \theta`

`\theta`

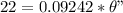
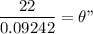
θ'' = 238.044 rad/s²

Thus; the angular acceleration is θ'' = 238.044 rad/s²