Answer:
16.87 m/s
Step-by-step explanation:
To find the speed of the car at the top, when the normal force is equal the gravitational force, we just need to equate both forces:
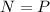
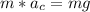
 is the centripetal acceleration in the loop:
is the centripetal acceleration in the loop:

So we have that:
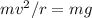
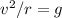
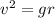
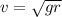
So, using the gravity = 9.81 m/s^2 and the radius = 29 meters, we have:
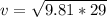

The speed of the car is 16.87 m/s at the top.