Question

Data on the modulus of elasticity obtained 1 minute after loading in a certain configuration and 4 weeks after loading for the same lumber specimens is presented here.

Observation 1 min 4 weeks Difference
1 10,779 9,875 904
2 16,620 13,250 3370
3 17,300 14,720 2580
4 15,830 12,713 3117
5 12,970 10,120 2850
6 17,260 14,570 2690
7 13,400 11,220 2180
8 13,099 11,858 1241
9 13,630 11,420 2210
10 13,260 10,910 2350
11 14,370 12,110 2260
12 11,577 8,819 2758
13 15,470 12,590 2880
14 17,840 15,090 2750
15 14,070 10,550 3520
16 14,190 12,157 2033

Required:
Calculate and interpret an upper confidence bound for the true average difference between 1-minute modulus and 4-week modulus; first check the plausibility of any necessary assumptions. (Use α = 0.05. Round your answer to the nearest whole number.)

Answer 1

The Confidence Interval = (2180, 2782)

Lower Bound for the true average difference between 1-minute modulus and 4-week modulus = 2180

Upper Bound for the true average difference between 1-minute modulus and 4-week modulus = 2782

- The interval obtained represents the range of values that the true average difference between 1-minute modulus and 4-week modulus can take on.

Explanation:

The confidence interval for any distribution is the range of values that the true population mean can take on with some level of confidence.

It is given mathematically as

Confidence Interval = (Sample Mean) ± (Margin of Error)

The Margin of Error is the width of the confidence interval about the mean.

It is given mathematically as

Margin of Error = (Critical Value) × (Standard Error of the Mean)

Before anything, we first state the conditions necessary for the confidence interval calculated to be valid.

- The sample must be a random sample extracted from the population distribution using random sampling technique.

- The sample distribution must be normal or approximately normal and this is confirmed by knowing that the population distribution is normal or almost normal.

These two conditions are assumed to be plausible for this sample distribution.

Here, we need the confidence interval for the true average difference between 1-minute modulus and 4-week modulus.

So, before anything, we need to first fin the sample mean and standard deviation for the differences obtained from the sample specimens.

904, 3370, 2580, 3117, 2850, 2690, 2180, 1241, 2210, 2350, 2260, 2758, 2880, 2750, 3520, 2033

Mean = (Σx/N)

Σx = Sum of all the variables = 39693

N = Sample size = 16

Sample Mean = (39693/16) = 2480.8125

Standard deviation =
`\sqrt{(Σ(x - xbar)^(2))/(N-1)\\}`

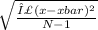
x = each variable

xbar = sample mean = 2480.8125

Note that we use (N-1) for the standard deviation because it is a sample standard deviation.

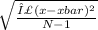`\sqrt{(Σ(x - xbar)^(2))/(N-1)\\}` = √(7227548.4375/15) = √(481836.5625)

= 694.14448243863 = 694.1445

Confidence Interval = (Sample Mean) ± (Margin of Error)

Margin of Error = (Critical Value) × (Standard Error of the Mean)

Confidence Interval = (Sample Mean) ± [(Critical Value) × (Standard Error of the Mean)]

Critical Value is obtained from the t-distribution table since no information on the population standard deviation is known.

For that, we need the significance level for the test and the degree of freedom.

Significance level = α = 0.05 (given in the question)

Degree of freedom = N - 1 = 16 - 1 = 15

t(0.05, 15) = 1.753 (from the t-distribution tables)

Standard error of the Mean = σₓ = (σ/
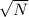`√(N)`) = (694.1445/
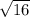`√(16)`) = 173.536125 = 173.536

Confidence Interval = (Sample Mean) ± [(Critical Value) × (Standard Error of the Mean)]

CI = (2480.8125) ± [(1.753 × 173.536)]

CI = (2480.8125) ± (301.09385)

CI = (2179.71865, 2781.90635)

CI = (2180, 2782)

This interval represents the range of values that the true average difference between 1-minute modulus and 4-week modulus can take on.

Hope this Helps!!!