Answer:
The requirements that are necessary for a normal probability distribution to be a standard normal probability distribution are µ = 0 and σ = 1.
Explanation:
A normal-distribution is an accurate symmetric-distribution of experimental data-values.
If we create a histogram on data-values that are normally distributed, the figure of columns form a symmetrical bell shape.
If X
 N (µ, σ²), then
N (µ, σ²), then
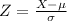 , is a standard normal variate with mean, E (Z) = 0 and Var (Z) = 1. That is, Z
, is a standard normal variate with mean, E (Z) = 0 and Var (Z) = 1. That is, Z
 N (0, 1).
N (0, 1).
The distribution of these z-variates is known as the standard normal distribution.
Thus, the requirements that are necessary for a normal probability distribution to be a standard normal probability distribution are µ = 0 and σ = 1.