Question

Sylvie finds the solution to the system of equations by graphing.

y = A system of equations. y equals StartFraction 2 over 3 EndFraction x plus 1. y equals negative StartFraction 2 over 3 EndFraction x minus 1x + 1 and y = x – 1

Which graph shows the solution to Sylvie’s system of equations?

A coordinate grid with 2 lines. The first line passes through the points (negative 1.7, 1.57), (0, negative 1), and (2, negative 4). The second line passes through the points (negative 1.7, 1.57), (0, 1), and (3, 0).

A coordinate grid with 2 lines. The first line passes through the points (negative 1.02, 0.63), (0, negative 1), and (2, negative 4). The second line passes through the points (negative 1.02, 0.63), (0, 1), and (3, 2).

A coordinate grid with 2 lines. The first line passes through the points (negative 1.5, 0), (0, negative 1), and (3, negative 3). The second line passes through the points (negative 1.5, 0), (0, 1), and (3, 3).

A coordinate grid with 2 lines. The first line passes through the points (negative 1.71, 0.14), (0, negative 1), and (3, negative 3). The second line passes through the points (negative 1.71, 0.14), (0, 1), and (2, 2).

Answer 1

D

Explanation:

trust

Answer 2

The correct answer is:

A coordinate grid with 2 lines. The first line passes through the points (negative 1.5, 0), (0, negative 1), and (3, negative 3). The second line passes through the points (negative 1.5, 0), (0, 1), and (3, 3).

Explanation:

We are given the system of equations as:

`1.\ y=-(2)/(3)x-1\\2.\ y=(2)/(3)x+1\\`

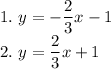
We have 2 equations here with variables x and y so we use coordinate grid with 2 lines having axis as x and y.

As per the given options, we can see that coordinate of one point has y = 0 and other point has x = 0.

So, let us put y = 0 and x =0, in both the equations one by one and have a look at the value of x coordinate.

y = 0, Equation (1) becomes:

`0=-(2)/(3)x-1\\\Rightarrow 1 =-(2)/(3)x\\\Rightarrow x = - 1.5`

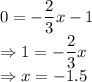
So, one coordinate is (-1.5, 0)

x = 0, Equation (1) becomes:

`y=-(2)/(3)* 0-1\\\Rightarrow y =-1`

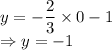
So, other coordinate is (0, -1)

And the point (3, -3) also satisfies the given equation.

y = 0, Equation (2) becomes:

`0=(2)/(3)x+1\\\Rightarrow 1 =-(2)/(3)x\\\Rightarrow x = - 1.5`

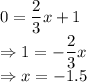
So, one coordinate is (-1.5, 0)

x = 0, Equation (2) becomes:

`y=(2)/(3)* 0+1\\\Rightarrow y =1`

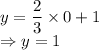
So, other coordinate is (0, 1)

And the point (3, 3) also satisfies the given equation.

Please refer to the attached graph and points on lines.

So, correct answer is:

A coordinate grid with 2 lines. The first line passes through the points (negative 1.5, 0), (0, negative 1), and (3, negative 3). The second line passes through the points (negative 1.5, 0), (0, 1), and (3, 3).