Question

PLEASE ANSWER FAST!! THANK YOU :)

Answer 1

option 1 both statements are true

Explanation:

Prove by PMI -- Principle of Mathematical Induction

1) n³ + 2n

n= 1 , 1³ +2*1 = 1+2 = 3 = 3*1 ---->divisible by 3

n = 2 ; 2³ + 2*2 = 8+4 = 12 = 3*4 ----> is divisible by 3

Assume that It is valid for n = k ;

`k^(3)+2k` = 3*m -----(I) , for all m ∈ N

We have to prove for n =k +1 , the statement is true.

n = k+1,
`(k+1)^(3)+2(k +1) =k^(3)+3k^(2)+3k +1 +2k +2`

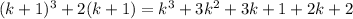
= k³ + 3k² + 3k + 3 + 2k

= k³ + 2k + 3k² + 3k + 3

= 3m + 3 (k² + k + 1)

= 3(3 + [k² + k + 1] ) is divisible by 3

Therefore, this statement is true

2)
`5^(2n)-1\\`

`n=1 ; 5^(2)-1 = 25 -1 = 24 divisible by 24\\\\n = 2 ; 5^(2*2)-1 = 5^(4)-1 = 625 - 1 = 624 divisible by 24`

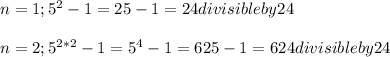
This statement is also true