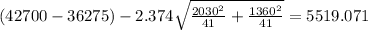Question

Use the following data to compute a 98% upper confidence bound for μ1 − μ2:

m = 41
x = 42,700
s1 = 2030
n = 41
y = 36,275
s2 = 1360.

Answer 1

`(42700- 36275) -2.374 \sqrt{(2030^2)/(41) +(1360^2)/(41)}= 5519.071`

`(42700- 36275) +2.374 \sqrt{(2030^2)/(41) +(1360^2)/(41)}=7330.929`

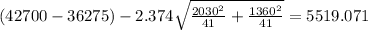
Explanation:

For this case we have the following info given:

`n_1 = 41 , \bar X_1 =42700 , s_1 = 2030`

`n_2 = 41 , \bar X_2 =36375 , s_2 = 1360`

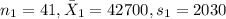
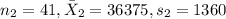
And for this case we want a 98% confidence interval. The significance would be:

`\alpha= 1-0.98=0.02`

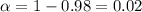
The degrees of freedom are:

`df = n_1 +n_2 -2= 41+41 -2= 80`

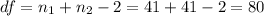
And the critical value for this case is:

`t_(\alpha/2)= 2.374`

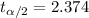
And the confidence interval would be given by:

`(\bar X_1 -\bar X_2) \pm t_(\alpha/2) \sqrt{(s^2_1)/(n_1)+(s^2_2)/(n_2)}`

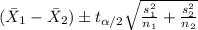
And replacing we got:

`(42700- 36275) -2.374 \sqrt{(2030^2)/(41) +(1360^2)/(41)}= 5519.071`

`(42700- 36275) +2.374 \sqrt{(2030^2)/(41) +(1360^2)/(41)}=7330.929`