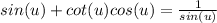Answer:
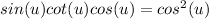
Step-by-step explanation:

First, let us simplify cot(u) as follows:
cot (u) =

also,
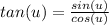
∴
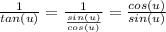
Hence the original expression becomes:

Next, sin(u) will cancel each other out, leaving the expression below:

hence:
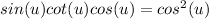
I also found a similar expression with a plus (+) sign after the "sin(u)" online, and if this was your question, the solution will be as follows:
sin(u)+ cot(u) cos(u)
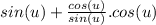
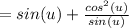
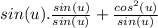 (note that
(note that
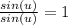 , hence multiplying it with sin(u) does not change anything in the expression.)
, hence multiplying it with sin(u) does not change anything in the expression.)
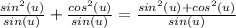
Now the relationship sin²(u) + cos²(u) = 1
Therefore:
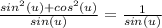
Hence,