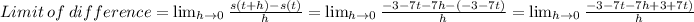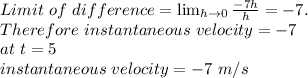Answer:
-7 m/s
Explanation:
The limit of the difference quotient is used to find the slope passing through two point. It is gotten by taking the limit as h approaches zero. It is given by:
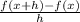
Given that:
The function s(t) = -3 - 7t
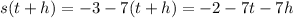 .
.
Using the limit of the difference quotient formula: