Question

A dairy farmer plans to enclose a rectangular pasture adjacent to a river. To provide enough grass for the herd, the pasture must contain 304,200 square meters. No fencing is required along the river. What dimensions will use the least amount of fencing

Answer 1

390 m (perpendicular to river) x 780 m (parallel to river)

Explanation:

Let y be the length of the side parallel to the river, and let x be the length of the sides perpendicular to the river.

The total area and length of fence required are given by:

`A=304,200=xy\\y=(304,200)/(x) \\L=2x+y`

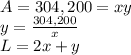
Rewriting the length of fence as a function of only x:

`L=2x+(304,200)/(x)`

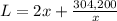
The value of x for which the derivate of L(x) is zero is the length of x that uses the least amount of fencing:

`L=2x+(304,200)/(x)\\(dL)/(dx)=2- (304,200)/(x^2)=0\\x^2=152,100\\x=390`

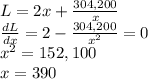
If x = 390 m, then:

`y=(304,200)/(390)\\y=780`

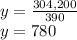
The dimensions that will use the least amount of fencing are 390 m x 780 m