Question

Using the digits 1 to 9, at most one time each, fill in the boxes so that the points make a parallelogram. Mathematically, use parallel line or congruent sides to explain your answer. If there are calculations, include those in your explanation.

Answer 1

`\left\begin{array}{ccc}A\left( \boxed{3} , \boxed{8} \right)&B\left( \boxed{9} , \boxed{6} \right )\\\\C\left( \boxed{1} , \boxed{4} \right)&D\left( \boxed{7} , \boxed{2} \right )\end{array}\right`

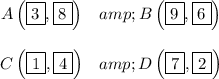
Explanation:

The coordinates are:

`\left\begin{array}{ccc}A\left( \boxed{3} , \boxed{8} \right)&B\left( \boxed{9} , \boxed{6} \right )\\\\C\left( \boxed{1} , \boxed{4} \right)&D\left( \boxed{7} , \boxed{2} \right )\end{array}\right`

The parallelogram is attached below.

To verify if these coordinates form a parallelogram, we show that:

• AB=CD; and
• AC=BD

Using Distance Formula

`AB = √((6-8)^2+(9-3)^2) = √((-2)^2+(6)^2) = √(40) $ units`

`CD = √((2-4)^2+(7-1)^2) = √((-2)^2+(6)^2) = √(40) $ units`

`AC = √((8-4)^2+(3-1)^2) = √((4)^2+(2)^2) = √(20) $ units`

`BD = √((6-2)^2+(9-7)^2) = √((4)^2+(2)^2) = √(20) $ units`

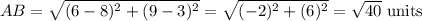
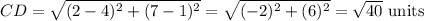
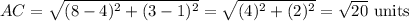
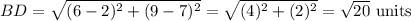
Since AB=CD; and AC=BD, the coordinates A, B, C, and D form the vertex of a parallelogram.