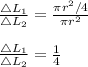Question

Two solid rods have the same length and are made of the same material with circular cross sections. Rod 1 has a radius 1 and Rod 2 has a radius 2=1/2 . If a compressive force is applied to both rods, their lengths are reduced by Δ1 and Δ2 , respectively.

Answer 1

Complete Question:

Two solid rods have the same length and are made of the same material with circular cross sections. Rod 1 has a radius r, and rod 2 has a radius r / 2. If a compressive force F is applied to both rods, their lengths are reduced by ΔL1 and ΔL2, respectively. The ratio ΔL1 / ΔL2 is equal to.

Answer:

`(\triangle L_1)/(\triangle L_2) =(1)/(4)`

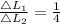
Step-by-step explanation:

Since the two rods have the same length, L₁ = L₂ = L

Radius of rod 1, r₁ = r

Radius of rod 2, r₂ = r/2

Cross sectional area of rod 1,
`A_1 = \pi r^2`

Cross sectional area of rod 2,
`A_2 = (\pi r^2)/(4)`

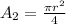
The same compressive force is applied to the two rods, F₁ = F₂ = F

The rods are said to be made of the same material, this means that they have the same young's modulus.

Young's modulus of rod 1,
`Y_1 = (FL)/(A_1 \triangle L_1)`

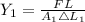
Young's modulus of rod 2,
`Y_2 = (FL)/(A_2 \triangle L_2)`

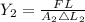
Since Y₁ = Y₂

`(FL)/(A_1 \triangle L_1) = (FL)/(A_2 \triangle L_2)\\\\ (1)/(A_1 \triangle L_1)= (1)/(A_2 \triangle L_2)\\\\`

`(\triangle L_1)/(\triangle L_2) = (A_2)/(A_1)\\`..............(*)

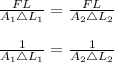
Put A₁ and A₂ into (*)

`(\triangle L_1)/(\triangle L_2) = (\pi r^2/4 )/(\pi r^2)\\\\(\triangle L_1)/(\triangle L_2) =(1)/(4)`