Question

You are given the following equation.

4x2 + 49y2 = 196

a. Find dy / dx by implicit differentiation.
dy / dx = _________

b. Solve the equation explicitly for y and differentiate to get dy/dx in terms of x. (Consider only the first and second quadrants for this part.)

dy / dx = ________

c. Check that your solutions to parts (a) and (b) are consistent by substituting the expression for y into your solution for part (a).

Answer 1

Explanation:

Given the equation 4x²+ 49y² = 196

a) Differentiating implicitly with respect to y, we have;

`8x + 98y(dy)/(dx) = 0\\98y(dy)/(dx) = -8x\\49y(dy)/(dx) = -4x\\(dy)/(dx) = (-4x)/(49y)`

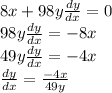
b) To solve the equation explicitly for y and differentiate to get dy/dx in terms of x,

First let is make y the subject of the formula from the equation;

If 4x²+ 49y² = 196

49y² = 196 - 4x²

`y^(2) = (196)/(49) - (4x^(2) )/(49) \\y = \sqrt{(196)/(49) - (4x^(2) )/(49) \\} \\`

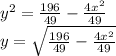
Differentiating y with respect to x using the chain rule;

Let
`u= (196)/(49) - (4x^(2) )/(49)`

`y = √(u) \\y =u^(1/2) \\`

`(dy)/(dx) = (dy)/(du) * (du)/(dx)`

`(dy)/(du) = (1)/(2)u^(-1/2) \\`

`(du)/(dx) = 0 - (8x)/(49) \\(du)/(dx) =(-8x)/(49) \\(dy)/(dx) = (1)/(2) ( (196)/(49) - (4x^(2) )/(49))^(-1/2) * (-8x)/(49)\\(dy)/(dx) = (1)/(2) ( (196-4x^(2) )/(49))^(-1/2) * (-8x)/(49)\\(dy)/(dx) = (1)/(2) ( \sqrt{ (49)/(196-4x^(2) ))} * (-8x)/(49)\\(dy)/(dx) = (1)/(2) *{ \frac{7}\sqrt {196-4x^(2) }} * (-8x)/(49)\\`

`(dy)/(dx) = \frac{-4x}{7\sqrt{196-4x^(2) } }`

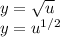
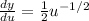
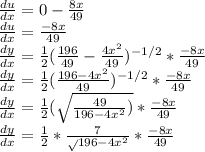
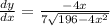
c) From the solution of the implicit differentiation in (a)

`(dy)/(dx) = (-4x)/(49y)`

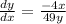
Substituting
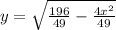`y = \sqrt{(196)/(49) - (4x^(2) )/(49) \\` into the equation to confirm the answer of (b) can be shown as follows

`(dy)/(dx) = \frac{-4x}{49\sqrt{(196-4x^(2) )/(49) } }\\(dy)/(dx) = \frac{-4x}{49\sqrt{196-4x^(2)}/7} }\\\\(dy)/(dx) = \frac{-4x}{7\sqrt{196-4x^(2)}}`

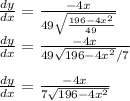
This shows that the answer in a and b are consistent.