Question

Consider the following distribution of objects: a 2.00-kg object with its center of gravity at (0, 0) m, a 2.20-kg object at (0, 5.00) m, and a 3.40-kg object at (2.00, 0) m. Where should a fourth object of mass 6.00 kg be placed so that the center of gravity of the four-object arrangement will be at (0, 0)?

Answer 1

body position 4 is (-1,133, -1.83)

Step-by-step explanation:

The concept of center of gravity is of great importance since in this all external forces are considered applied, it is defined by

x_cm = 1 /M ∑
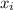`x_(i)` m_{i}

y_cm = 1 /M ∑ y_{i} mi

Where M is the total mass of the body, mi is the mass of each element

give us the mass and position of this masses

body 1

m1 = 2.00 ka

x1 = 0 me

y1 = 0 me

body 2

m2 = 2.20 kg

x2 = 0m

y2 = 5 m

body 3

m3 = 3.4 kg

x3 = 2.00 m

y3 = 0

body 4

m4 = 6 kg

x4=?

y4=?

mass center position

x_cm = 0

y_cm = 0

let's apply to the equations of the initial part

X axis

M = 2.00 + 2.20 + 3.40

M = 7.6 kg

0 = 1 / 7.6 (2 0 + 2.2 0 + 3.4 2 + 6 x4)

x4 = -6.8 / 6

x4 = -1,133 m

Axis y

0 = 1 / 7.6 (2 0 + 2.20 5 +3.4 0 + 6 y4)

y4 = -11/6

y4 = -1.83 m

body position 4 is (-1,133, -1.83)