Question

PLEASE HELP ME WITH THESE QUESTIONS!! :((( #2 & 4a)

Answer 1

2 a. 210 ways

b. 50 ways

c. 28 ways

d. 0.205

4 a. 1716 ways

Explanation:

2. a. The number of ways,
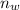`n_w` of selecting without restriction is given as follows;

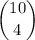`\dbinom{10}{4}` = 10!/(4!(10 - 4)!) = 210

b. The number of ways of selecting 3 boys from 5 is 5!/(3!(5 - 3)!) = 10 ways

The number of ways of selecting the remaining 1 girl from 5 = 5!/(1!(5 - 1)!) = 5 ways

The number of ways of the selection where there must be three boys = 5×10 = 50 ways

c. Given that Maggie and Marley must be chosen, each of whom can be chosen only one way, we have;

Selection of 2 from 8 gives;

8!/(2!(8 - 2)!) = 28

Therefore, the number of ways of the selection where there must be Maggie and Marley is 28 × 1 × 1 = 28 ways

d. The probability of no boys is given by the relation;

P(k success from n trials) =
`_nC_r \cdot p^k \cdot (1 - p)^(n-k)`

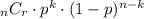
Where n = number of persons = 10

k = Number of person in the group = 4

p = Probability of success of girls = 1/2

Therefore, we have for no boys;

`\dbinom{10}{4} * \left ((1)/(2) \right )^4* \left (1-(1)/(2) \right )^(10-4) = (210)/(16 * 64) = (105)/(512) = 0.205`

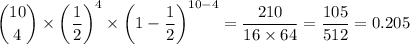
4a) The number of ways of selecting 9 softball players from 15 where Rylea and Emily must be included;

Given that Rylea and Emily are already selected, we have;

The number of ways of selecting 7 softball players from 13 given as follows;

13!/(7!(13 - 7)!) = 1716 ways

Given that Rylea and Emily can both be selected in only one way, the total number of ways = 1×1×1716 = 1716 ways