Answer:
![P(x \geq 3)=1- [P(X=0)+P(X=1) +P(X=2)]](https://img.qammunity.org/2021/formulas/mathematics/college/3aqnneawx5xbh8t8xw0d3ogra9dvwm7ira.png)
And we can find the individual probabilities like this:
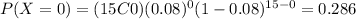
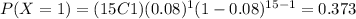
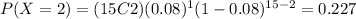
![P(x \geq 3)=1- [0.286+0.373+0.227]=0.114](https://img.qammunity.org/2021/formulas/mathematics/college/wqduc6iawb4gr2xuamj9fr7qmgaqmcskxk.png)
Explanation:
Let X the random variable of interest "number of cars involved in an accident", on this case we now that:
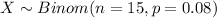
The probability mass function for the Binomial distribution is given as:
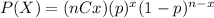
Where (nCx) means combinatory and it's given by this formula:
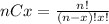
And we want to find this probability:
![P(x \geq 3)=1- [P(X=0)+P(X=1) +P(X=2)]](https://img.qammunity.org/2021/formulas/mathematics/college/3aqnneawx5xbh8t8xw0d3ogra9dvwm7ira.png)
And we can find the individual probabilities like this:
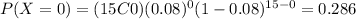
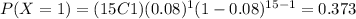
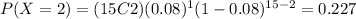
![P(x \geq 3)=1- [0.286+0.373+0.227]=0.114](https://img.qammunity.org/2021/formulas/mathematics/college/wqduc6iawb4gr2xuamj9fr7qmgaqmcskxk.png)